Simulating Neural Networks With Mathematica Ware

Posted By admin  On 19.05.21

Simulating neural networks with mathematica warehouseSimulating Neural Networks With Mathematica Ware

Simulating Neural Networks With Mathematica

  1. D. O. Hebb, The Organization of Behavior, a Neuropsychological Theory, John Wiley: New York, NY, 1949.Google Scholar
  2. B. Kosko, Neural Networks and Fuzzy Systems, Prentice-Hall: Englewood Cliffs, NJ, 1992.zbMATHGoogle Scholar
  3. F. Rosenblatt, “The perceptron: a probabilistic model for information storage and organization in the brain,” Psychology Review, vol. 65, pp. 386–408, 1958.MathSciNetCrossRefGoogle Scholar
  4. R. P. Lippmann, “An introduction to computing with neural nets,” IEEE Acoustics, Speech, and Signal Processing Magazine, pp. 4–22, April 1987.Google Scholar
  5. D. E. Rumelhart, J. L. McClelland, and the PDP Research Group, Parallel Distributed Processing, vol. 1, The MIT Press: Cambridge, MA, 1989.Google Scholar
  6. R. Hecht-Nielsen, Neurocomputing, Addison-Wesley Publishing Company: New York, NY, 1990.Google Scholar
  7. D. R. Hush and B. G. Home, “Progress in supervised neural networks,” IEEE Signal Processing Magazine, pp. 8–39, Jan. 1993.Google Scholar
  8. D. B. Parker, “Optimal algorithms for adaptive networks: second order back propagation, second order direct propagation, and second order heb-bian learning,” Proc. IEEE the First Inter. Conf. Neural Networks, vol. 2, pp. 593–600, San Diego, CA, 1987.Google Scholar
  9. R. A. Jacobs, “Increased rates of convergence through learning rate adaptation,” Neural Networks, vol. 1, pp. 295–307, 1988.CrossRefGoogle Scholar
  10. J. M. Zurada, Introduction to Artificial Neural Systems, West Publishing Company: New York, NY, 1992.Google Scholar
  11. R. L. Watrous, “Learning algorithms for connectionist networks: applied gradient methods of nonlinear optimization,” Proc. IEEE Inter. Conf. Neural Networks, vol. 2, pp. 619–627, June 1987.Google Scholar
  12. J. A. Freeman, Simulating neural networks with Mathematica, Addison-Wesley Publishing Company: New York, NY, 1994.Google Scholar
  13. Y. Le Cun, J. S. Denker, and S. A. Solla, “Optimal brain damage,” in Advances in Neural Information Processing Systems Vol. 2 (D. Touretzky, eds.) pp. 598–605, Morgan Kaufmann: San Mateo, CA, 1990.Google Scholar
  14. Y. Le Cun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, and L. D. Jackel, “Backpropagation applied to handwritten zip code recognition,” Neural Computation, vol. 1, no. 4, pp. 541–551, 1989.CrossRefGoogle Scholar
  15. J. J. Hopfield, “Neurons with graded response have collective computational properties like those of two state neurons,” Proc. National Academy of Science, vol. 81, pp. 3088–3092, 1984.CrossRefGoogle Scholar
  16. J. J. Hopfield and D. W. Tank, “Neural computation of decisions in optimization problems,” Biological Cybernetics, vol. 52, pp. 141–154, 1985.MathSciNetzbMATHGoogle Scholar
  17. D. W. Tank and J. J. Hopfield, “Simple ‘neural’ optimization networks: an A/D converter, signal decision circuit, and a linear programming circuit,” IEEE Trans. Circuits and Systems, vol. 33, no. 5, pp. 533–541, May 1986.CrossRefGoogle Scholar
  18. B. W. Lee and B. J. Sheu, Hardware Annealing in Analog VLSI Neuro-computing, Kluwer Academic Publisher: Boston, MA, 1991.CrossRefGoogle Scholar
  19. B. Kosko, “Bidirectional Associative Memories,” IEEE Trans. Systems, Man, and Cybernetics, vol. 18, no. 1, pp. 49–60, 1988MathSciNetCrossRefGoogle Scholar
  20. T. Kohonen, Self-Organization and Associative Memory, Springer-Verlag: Berlin Germany, 1984.zbMATHGoogle Scholar
  21. T. Kohonen, “The self-organizing map,” IEEE Proceeding, vol. 78, no. 9, pp. 1464–1480, 1990.CrossRefGoogle Scholar
  22. T. Serrano, S. Grossberg, “ART2: self-organization of stable category recognition codes for analog input patterns,” Applied Optics, vol. 26, no. 23, pp. 4919–4930, Dec. 1987.CrossRefGoogle Scholar
  23. G. A. Carpenter, S. Grossberg, D. B. Rosen, “Fuzzy ART: fast stable learning and categorization of analog patterns by an adaptive resonance system,” Neural Networks, vol. 4, pp. 759–771, 1991.CrossRefGoogle Scholar
  24. G. A. Carpenter, S. Grossberg, “ART3: hierarchical search using chemical transmitters in self-organizing pattern recognition architectures,” Neural Networks, vol. 3, pp. 129–152, 1990.CrossRefGoogle Scholar
  25. G. A. Carpenter, S. Grossberg, J. H. Reynolds, “ARTMAP: supervised real-time learning and classification of nonstationary data by a self-organizing neural network,” Neural Networks, vol. 4, pp. 565–588, 1991.CrossRefGoogle Scholar
  26. G. A. Carpenter, S. Grossberg, N. Markuzon, J. H. Reynolds, D. B. Rosen, “Fuzzy ARTMAP: a neural network architecture for incremental supervised learning of analog multidimensional maps,” IEEE Trans. on Neural Networks, vol. 3, no. 5, pp. 698–712, Sept. 1992.CrossRefGoogle Scholar
  27. G. F. Hinton, T. J. Sejnowski, and D. H. Ackley, “Boltzmann machines: constraint satisfaction networks that learn,” Carnegie Mellon University Technical Report, vol. CMU-CS-84-119, Carnegie Mellon University, Pittsburgh PA, May 1984.Google Scholar
  28. C. G. E. Boender, A. H. G. Rinnooy Kan, and G. T. Timmer, “A stochastic method for global optimization,” Mathematical Programming, vol. 22, pp. 125–140, 1982.MathSciNetzbMATHCrossRefGoogle Scholar
  29. D. H. Ackley, G. E. Hinton, and T. J. Sejnowski, “A learning algorithm for Boltzmann Machines,” Cognitive Science, vol. 9, pp. 147–168, Ablex Publishing Corporation: Norwood, NJ, 1985.Google Scholar
  30. S. Kullback, Information Theory and Statistics, Wiley: New York, NY, 1959.zbMATHGoogle Scholar

Mathematica Neural Network Example

Simulating Neural Networks With Mathematica Download Freeware. 6/3/2017 0 Comments A Resource for the Technical Computing Community. For more on popular topics, see MATLAB and Simulink product resources. For your computer project, you will do one of the following: 1) Devise a novel application for a neural network model studied in the course; 2) Write a program to simulate a model from the neural network literature; 3) Design and program a method for solving some.

Wolfram Neural Network

Mathematica

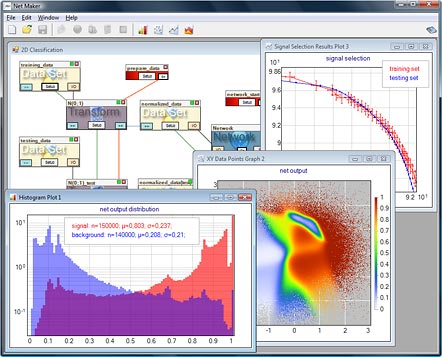
Simulating Neural Networks With Mathematica Warehouse

  1. Duncan, S.,Kurz, E.,Rivardo, M., &Strasser, R. (1996, November).Semantic priming in a simple two-layer neural network. Poster presented at 37th Annual Meeting of the Psychonomic Society, Chicago.Google Scholar
  2. Freeman, J. A. (1994).Simulating neural networks with Mathematica. New York: Addison-Wesley.Google Scholar
  3. Gronlund, S. D., Sheu, C.-F., &Ratcliff, R. (1990). Implementation of global memory models with software that does symbolic computation.Behavior Research Methods, Instruments, & Computers,22, 228–235.Google Scholar
  4. Hinton, G. E., McClelland, J. L., &Rumelhart, D. E. (1986). Distributed representations. In D. E. Rumelhart & J. L. McClelland (Eds.),Parallel distributed processing: Explorations in the microstructure of cognition. Vol. 1: Foundations (pp. 77–109). Cambridge, MA: MIT Press.Google Scholar
  5. Kim, C. &Myung, I. J. (1995). Incorporating real-time random time effects in neural networks: A temporal summation mechanism. In J. D. Moore & J. F. Lehman (Eds.),Proceedings of the Seventeenth Annual Conference of the Cognitive Science Society (pp. 472–477). Hillsdale, NJ: Erlbaum.Google Scholar
  6. Lorig, T. S., &Urbach, T. P. (1995). Event-related potential analysis usingMathematica.Behavior Research Methods, Instruments, & Computers,27, 358–366.CrossRefGoogle Scholar
  7. Masters, T. (1993).Practical neural network recipes in C++. San Diego: Academic Press.Google Scholar
  8. Ratcliff, R. (1994). Using computers in empirical and theoretical work in cognitive psychology.Behavior Research Methods, Instruments, & Computers,26, 94–106.Google Scholar
  9. Rumelhart, D. E., McClelland, J. L. (Eds.) (1986).Parallel distributed processing: Explorations in the microstructure of cognition. Vol. 1: Foundations. Cambridge, MA: MIT Press.Google Scholar
  10. Wolfram, S. (1994).Mathematica (Version 2.2.2) [Computer programming language]. Champaign, IL: Wolfram Research, Inc.Google Scholar
  11. Wolfram, S. (1996).Mathematica (Version 3) [Computer programming language]. Cambridge: Cambridge University Press.Google Scholar